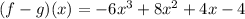Question

Can you show the answer and explain how u got it

Answer 1

GIVEN:

We are given the following functions;

`\begin{gathered} f(x)=3x^2+4x-6 \\ \\ g(x)=6x^3-5x^2-2 \end{gathered}`

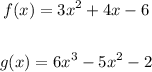
Required;

Find the value of;

`(f-g)(x)`

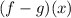
To solve the given problem, we apply the rule as shown below;

`\begin{gathered} Given:f(x)\text{ }and\text{ }g(x) \\ \\ (f-g)(x)=f(x)-g(x) \end{gathered}`

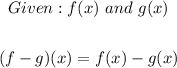
We can now substitute the values of each function into the refined expression and solve as follows;

`\begin{gathered} (f-g)(x)=3x^2+4x-6-(6x^3-5x^2-2) \\ \\ =3x^2+4x-6-6x^3+5x^2+2 \end{gathered}`

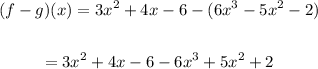
Notice how the minus sign is distributed into the terms in parenthesis on the right.

The negative terms now take on a positive value. We can now simplify further;

`\begin{gathered} (f-g)(x)=3x^2+4x-6-6x^3+5x^2+2 \\ \\ (f-g)(x)=-6x^3+3x^2+5x^2+4x-6+2 \\ \\ (f-g)(x)=-6x^3+8x^2+4x-4 \end{gathered}`

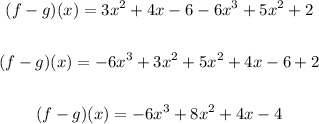
ANSWER:

Option A is the correct answer.

`(f-g)(x)=-6x^3+8x^2+4x-4`