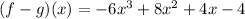GIVEN:
We are given the following functions;
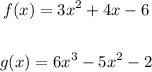
Required;
Find the value of;
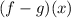
To solve the given problem, we apply the rule as shown below;
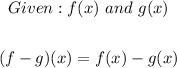
We can now substitute the values of each function into the refined expression and solve as follows;
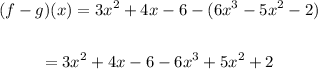
Notice how the minus sign is distributed into the terms in parenthesis on the right.
The negative terms now take on a positive value. We can now simplify further;
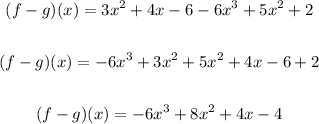
ANSWER:
Option A is the correct answer.