Question

I’m so stuck I really don’t know consumers math for real

Answer 1

We are going to be working on the two(2) data sets separately, as they relate to the options given.

For option A, we are going to find the median of the two(2) data set.

Thus, we have:

`\begin{gathered} \text{For Non-fiction:} \\ \text{Data set:13,13,13,17,18,18} \\ \text{Median}=(13+17)/(2) \\ \text{Median}=(30)/(2)=15 \end{gathered}`

The median number of fiction books is Not the same as the median number of Non-fiction books. Hence, option A is NOT true

For option B, we are going to find the range of the data set for Non-fiction books.

`\begin{gathered} \text{Range of a data set=Highest data - Lowest data} \\ \text{For the Non-fiction data;} \\ \text{Highest data=}18 \\ \text{Lowest data=13} \\ \text{Range}=18-13=5 \end{gathered}`

The range for the number of Non-fiction books is 5 and NOT 18. Hence, option B is NOT true.

For option C, we are going to find the range of all the data set combined.

`\begin{gathered} \text{For the combined data:} \\ \text{Range}=19-10=9 \end{gathered}`

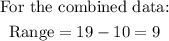
The range of data is NOT 1 greater for the non fiction books. Hence, option C is NOT true

The correct option is option D, as we have earlier obtained the median number for the fictions books to be 14.5, as shown above while solving for option A