We are going to be working on the two(2) data sets separately, as they relate to the options given.
For option A, we are going to find the median of the two(2) data set.
Thus, we have:
![\begin{gathered} \text{For Fiction:} \\ \text{Data set: 10,12,14,}15,15,19 \\ \text{Median of a data set is the middle data. Data must be arranged in ascending order or descending order} \\ In\text{ this case},\text{ there are two(2) data at the middle, hence we find the average of the data set.} \\ \text{Therefore, Median =}(14+15)/(2) \\ \text{Median}=(29)/(2)=14.5 \end{gathered}]()

The median number of fiction books is Not the same as the median number of Non-fiction books. Hence, option A is NOT true
For option B, we are going to find the range of the data set for Non-fiction books.

The range for the number of Non-fiction books is 5 and NOT 18. Hence, option B is NOT true.
For option C, we are going to find the range of all the data set combined.
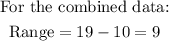
The range of data is NOT 1 greater for the non fiction books. Hence, option C is NOT true
The correct option is option D, as we have earlier obtained the median number for the fictions books to be 14.5, as shown above while solving for option A