Question

An artist has been commissioned to make a stained glass window in the shape of a regular octagon. The octagon must fit inside aPlease check photo

Answer 1

Given:

Length of each side of the square = 12 in

Let's find the length of each side of the regular octagon.

We can see the parts of the rectangle which are not a part of the octagon for right triangles.

Since the two legs are equal, this means the triangle is a 45-45-90 degrees special right triangle.

Now, apply Pythagorean theorem:

`x^2+x^2=y^2`

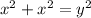
Also, we know the length of the two sides plus one leg of the octagon equals length of one side of the square.

Now, we have the second equation:

`x+x+y=12`

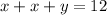
Now, let's solve both equations simultaneously:

`\begin{gathered} x^2+x^2=y^2 \\ x+x+y=12 \end{gathered}`

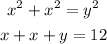
Solving further, we have:

`\begin{gathered} 2x^2=y^2 \\ 2x+y=12 \end{gathered}`

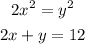
In the first equation take the square root of both sides:

`\begin{gathered} √(2x^2)=√(y^2) \\ \\ x√(2)=y \\ \\ y=x√(2) \end{gathered}`

Now, substitute x√2 for y in the second equation:

`\begin{gathered} 2x+y=12 \\ \\ 2x+x√(2)=12 \end{gathered}`

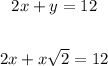
Factor out x:

`x(2+√(2))=12`

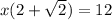
Divide each term by (2+√2):

`\begin{gathered} (x(2+√(2)))/(2)=(12)/(2+√(2)) \\ \\ x=3.5 \end{gathered}`

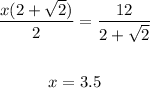
Now, to find the length of reach side of the octagon, given that the length of the leg of the triangle is 3.5, apply Pythagorean theorem:

`\begin{gathered} y=√(3.5^2+3.5^2) \\ \\ y=√(12.25+12.25) \\ \\ y=√(24.50) \\ \\ y=4.9\approx5 \end{gathered}`

Therefore, each side of the octagon is approximately 5 in.

ANSWER:

5 in