Question

Find the volume of the figure. Use 3.14 for π and round to the nearest hundredth, if necessary.

Answer 1

Observe the given figure carefully.

It is a composite cylinder with a hemisphere placed at the top.

The radius of the hemisphere is the same as the radius of the cylinder,

`r=9\text{ yd}`

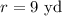
The height of the cylindrical part is 5 yards,

`h=5\text{ yd}`

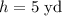
Consider the formulae,

`\begin{gathered} \text{Volume of cylinder}=\pi r^2h \\ \text{Volume of hemisphere}=(2)/(3)\pi r^3 \end{gathered}`

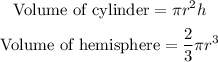
Consider that the volume of the composite figure will be the sum of the volume of cylindrical and the volume of the hemispherical part,

`\begin{gathered} \text{ Total Volume}=\text{ Volume of cylindrical part}+\text{ Volume of hemispherical part} \\ V=\pi r^2h+(2)/(3)\pi r^3 \end{gathered}`

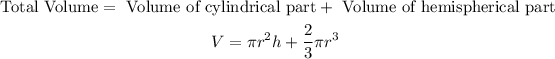
Substitute the values,

`\begin{gathered} V=\pi(9)^2(5)+(2)/(3)\pi(9)^3 \\ V=405\pi+486\pi \\ V=891\pi \\ V=891(3.14) \\ V=2797.74 \end{gathered}`

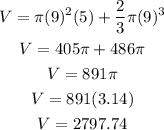
Thus, the required volume of the given composite figure is 2797.74 cubic yards.