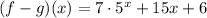Find (f -g)(x) if f(x) = 4.5* + 15x - 7 and g(x)=(-3). 5* - 13.

Question

asked Oct 9, 2023 162k views

1 Answer

Neilfws · Answer 1 · 2023-10-14T12:33:40+0000

You have the following function given in the exercise:

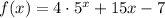
$f\mleft(x\mright)=4\cdot5^x+15x-7$

And the other function is:

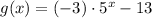
$g\mleft(x\mright)=\mleft(-3\mright)\cdot5^x-13$

You need to remember that this means that you must subtract the function g(x) from the function f(x):

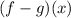
$\mleft(f-g\mright)\mleft(x\mright)$

It can also be expressed as following:

Then, you can set up that:

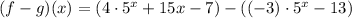
$(f-g)(x)=(4\cdot5^x+15x-7)-((-3)\cdot5^x-13)$

In order to simplify, it is important to remember the Sign rules for Multiplication:

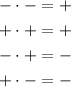
$\begin{gathered} -\cdot-=+ \\ +\cdot+=+ \\ -\cdot+=- \\ +\cdot-=- \end{gathered}$

Then, you can distributive the negative sign:

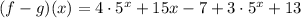
$(f-g)(x)=4\cdot5^x+15x-7+3\cdot5^x+13$

Finally, you need to add the like terms (which are defined as those terms that have the same variables and the same exponents):

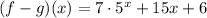
$(f-g)(x)=7\cdot5^x+15x+6^{}$

The answer is:

$(f-g)(x)=7\cdot5^x+15x+6^{}$