Question

The number of bacteria in a culture is given by the function N(t)=975e^.3twhere t is measured in hours.(a) What is the relative rate of growth of this bacterium population?(b) What is the initial population of the culture (at t=0)?(c) How many bacteria will the culture contain at time t=5?

Answer 1

Step-by-step explanation

Since we have the function:

`N(t)=975e^(0.3t)`

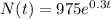
The standard form of a growth equation is the following:

`N(t)=N_0*e^(kt)`

Where N_0 = Initial population k= relative growth rate

a) The relative rate of growth is k=0.3

b) The initial population is 975 bacteria.

c) Plugging in the value t=5 into the expression:

`N(t)=975*e^(0.3*5)`

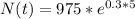
Multiplying numbers:

`N(t)=975*e^(1.5)`

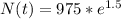
Computing the exponent:

`N(t)=975*4.48`

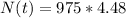
Multiplying terms:

`N(t)=4368`

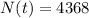
There will be 4368 bacteria at the time t=5