Question

Can someone help me with this geometry question it’s a 2 part so it’s one big question please

Answer 1

Part A

Equation of a circle is given as

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \text{Where (h, k) are center cordinates and r = radius } \end{gathered}`

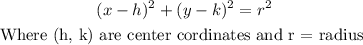
So for circle A, center (0, 0) and radius 6, the equation of the circle is

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-0)^2+(y-0)^2=6^2 \\ x^2+y^2=36 \end{gathered}`

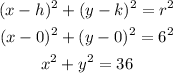
For circle B, center (-4, -2) and radius 4, the equation of the circle is

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-(-4)^2+(y-(-2)^2=4^2 \\ (x+4)^2+(y+2)^2=16 \end{gathered}`

Making the graphs, we have

So the large green circle is for A and the smaller Blue circle is for B

Part B

The sequence of transformations that maps circle B unto circle A

We can see that circle B is smaller than circle A, that means circle B was derived from circle A being shrinked.

Now, from their radii, circle A is 6 units and circle B is 4 units. So the scale factor is

`(4)/(6)=(2)/(3)`

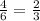
So, the transformation a dilation; circle A was shrinked by a scale factor less than 1.

Also We can see that a shift was noticed. 4 units to the left and 2 units down.

Hence the answer is

The transformation is a dilation; circle A was shrinked by a scale factor less than 1 and was shifted 4 units to the left and 2 units down.