Question

I want to find step by step answers for these questions pls

Answer 1

Answers:

a) midpoint: (1, 4)

b) slope of PQ: 1/3

c) length of PQ: √40

d) equation of perpendicular bisector of PQ:

Step-by-step explanation:

The given points are P(4, 5) and Q(-2, 3)

Part a)

The midpoint of two points (x1, y1) and (x2, y2) can be calculated as

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

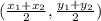
So, replacing (x1, y1) = P(4, 5) and (x2, y2) = Q(-2, 3), we get:

`((4+(-2))/(2),(5+3)/(2))=((2)/(2),(8)/(2))=(1,4)`

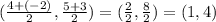
Then, the midpoint of PQ is (1, 4)

Part b)

The slope of a segment that passes through points (x1, y1) and (x2, y2) can be calculated as

`\text{slope}=(y_2-y_1)/(x_2-x_1)`

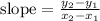
Replacing (x1, y1) = P(4, 5) and (x2, y2) = Q(-2, 3), we get:

`\text{slope}=(3-5)/(-2-4)=(-2)/(-6)=(1)/(3)`

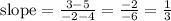
So, the slope is 1/3

Part c)

The length of a segment that goes from (x1, y1) to (x2, y2) is calculated as

`\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Replacing (x1, y1) = P(4, 5) and (x2, y2) = Q(-2, 3), we get:

`\begin{gathered} \sqrt[]{(-2-4)^2+(3-5)^2} \\ \sqrt[]{(-6_{})^2+(-2)^2} \\ \sqrt[]{36+4} \\ \sqrt[]{40} \end{gathered}`

Therefore, the length of PQ is √40.

Part d)

The perpendicular bisector of PQ is a line that divides the segment into two equal and forms a 90 degrees angle with the segment.

First, we need to calculate the slope of the line. Taking into account that the slope of perpendicular lines multiply to -1, we get that the slope of the perpendicular bisector is

`\begin{gathered} m\cdot(1)/(3)=-1 \\ m\cdot(1)/(3)\cdot3=-1\cdot3 \\ m=-3 \end{gathered}`

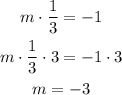
Additionally, the perpendicular bisector will pass through the midpoint of PQ, so it will pass through (1, 4).

Now, the equation of a line with slope m= -3 that passes through the point (x1, y1) = (1, 4) is

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4=-3(x-1) \\ y-4=-3x-3(-1) \\ y-4=-3x+3 \\ y-4+4--3x_{}+3+4 \\ y=-3x+7 \end{gathered}`

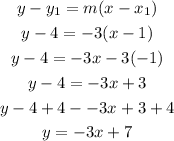
Therefore, the equation of the perpendicular bisector is y = -3x + 7.