EXPLANATION
As we already know, the slope formula will be as follow:
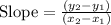
Let's consider:
Point A: (x1,y1)= (-5,5) and Point B: (x2,y2)=(-2,2)
Replacing these two ordered pais in slope formula:
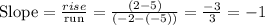
The slope of AB is -1.
Therefore, as BC and AC is a part of the same line trend, the slope of both ordered pairs will be the same.
1) Slope of AB : -1
2) Slope of BC :-1
3) Slope of AC :-1
Describe the Slope of the line:
This slope is negative and the line is downwards.