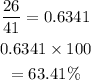Question

One coin is picked at random. What is the probability of not picking a penny? Round the answer the nearest hundredth of a percent.

Answer 1

The probability of not picking a penny is the probability of picking a penny SUBTRACTED from 1.

We can write it as:

P(not Penny) = 1 - P(penny)

There are

7 + 11 + 8 + 15 = 41 coins altogether

There are 15 pennies. Thus, probability of penny is:

P(penny) = 15/41

Now,

Probability of Not picking a Penny is:

P(not Penny) = 1 - P(penny)

P(not Penny) = 1 - 15/41

P(not penny) = 26/41

To get percentage, we divide and then multiply by 100 and tag along a '%' sign.

So,

`\begin{gathered} (26)/(41)=0.6341 \\ 0.6341*100 \\ =63.41\% \end{gathered}`