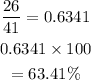The probability of not picking a penny is the probability of picking a penny SUBTRACTED from 1.
We can write it as:
P(not Penny) = 1 - P(penny)
There are
7 + 11 + 8 + 15 = 41 coins altogether
There are 15 pennies. Thus, probability of penny is:
P(penny) = 15/41
Now,
Probability of Not picking a Penny is:
P(not Penny) = 1 - P(penny)
P(not Penny) = 1 - 15/41
P(not penny) = 26/41
To get percentage, we divide and then multiply by 100 and tag along a '%' sign.
So,