We know that Jack has narrowed down his selection to a total of:
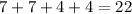
items.
Since he wants all the cheeses and he wants to use the express lane he needs to select a total of:
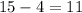
more items.
From the total number of items he will select:
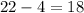
items.
Then he needs to select 11 item from 18 possible items. To determine in how many ways can do this we can use a combination, a combination is given by:
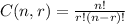
Then we have:
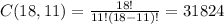
Therefore, there are 31824 ways Jack can choose 15 items if he wants all the cheeses