The number of proper subset of a set N is given as;
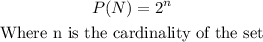
The cardinality of a set is the number of elements in a set.
Then, given the set;
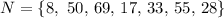
The cardinality n, is7 because there are seven elements in the set.
Then, the number of proper subsets is;
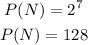
Thus, the set N has 128 distinct proper subsets.