SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question.
STEP 1: Interpret the statements
Let the tickets for a one-hour tour be represented by x
Let the tickets for a two-hour tour be represented by y
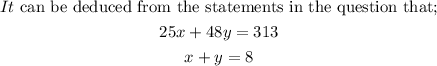
STEP 2: Solve the derived equations simultaneously
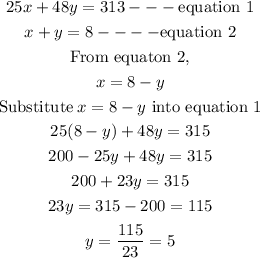
STEP 3: Get the value of x

Hence,
the number of tickets for a one-hour tour bought is 3
the number of tickets for a two-hour tour bought is 5