Question

In a triangle ABC, a line BP is drawn from B so that P lies on the side AC. For the triangle, AP=27mm, BP=30mm, BC=82mm and the angle APB=76∘ apply. Determine the area of triangle ABC

Answer 1

The diagram for this is shown below

From the diagram above, considering triangle BPC, let us find angle C

Using sine rule, we have

`\begin{gathered} (sinC\degree)/(30)=(sin104\degree)/(82) \\ sinC=(30* sin104\degree)/(82) \\ C=sin^(-1)(30sin104)/(82) \\ C=20.79\degree \end{gathered}`

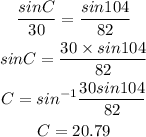
From the same triangle BPC to get angle B, we have

`\begin{gathered} B+P+C=180\degree \\ B+104+20.79=180 \\ B+124.79=180 \\ B=55.21\degree \end{gathered}`

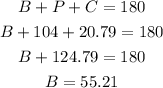
From the same triangle BPC, using sine rule to get the side PC, which I called x, we have

`\begin{gathered} (sinB)/(x)=(sinP)/(82) \\ (sin55.21\degree)/(x)=(sin104\degree)/(82) \\ x=(sin55.21*82)/(sin104\degree) \\ x=69.404mm \end{gathered}`

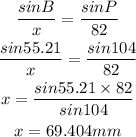
This makes the side AC to become

`27+69.404=96.404mm`

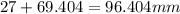
So, to get the area of the triangle ABC, we have that

`Area=(1)/(2)|AC|*|BC|* sinC`

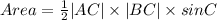
Applying we have

`\begin{gathered} Area=(1)/(2)|96.404|*|82|* sin20.79\degree \\ =1402.94mm^2 \end{gathered}`

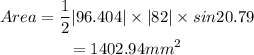
Hence the answer is approximately 1402.94 square-millimeters to the nearest hundredth