We have the function that relates x and y expressed as:
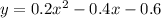
a) We have to find the x-intercepts.
To do that we can use the quadratic equation:
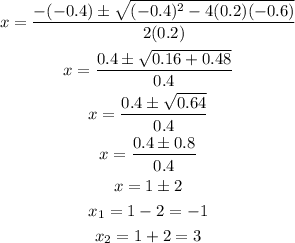
Then, we have x-intercepts at x = -1 and x = 3.
b) We have to find the vertex.
We can find the x-coordinate of the vertex using the linear coefficient b = -0.4 and the quadratic coefficient a = 0.2:
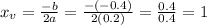
It can also be calculated as the average of the x-intercepts.
Knowing the x-coordinate of the vertex, we can find the y-coordinate of teh vertex using the formula applied to x = 1:
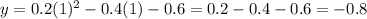
Then, the vertex is (1, -0.8).
c) The minimum height will be given by the y-coordinate of the vertex.
Relative to the horizontal axis (y = 0), the minimum height will be -0.8 meters below that level.
Answer:
a) The x-intercepts are x = -1 and x = 3.
b) The vertex is (1,-0.8)
c) The minimum height is 0.8 units below the horizontal axis.