Question

The age of children in kindergarten on the first day of school is uniformly distributed between 5 and5.76 years old. A first time kindergarten child is selected at random. Round answers to 4 decimalplaces if possible.a. The mean of this distribution isb. The standard deviation isC. The probability that the the child will be older than 5 years old?d. The probability that the child will be between 5.4 and 5.6 years old ise. If such a child is at the 53rd percentile, how old is that child?years old.CalculatorScratchwork Area

Answer 1

Given the interval of the distribution as

`5-5.76`

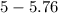
a) To find the mean, we will calculate the mid-value of the interval, this is shown below

Hence, the mean is 5.38

b) To find the standard deviation

`\begin{gathered} SD=\sqrt[]{((b-a)^2)/(12)} \\ b=5.76 \\ a=5 \\ SD=\sqrt[]{((5.76-5)^2)/(12)} \\ =\sqrt[]{(0.76^2)/(12)}=0.2194 \end{gathered}`

Hence, the standard deviation is 0.2194

c) The probability that the child will be older than 5 years will be

`P(older\text{ than 5 years)=}(5.76-5)/(5.76-5)=(0.76)/(0.76)=1.0`

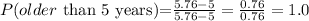
Hence, the probability that the child will be older than 5 years is 1.0

d) The probability that the child age is between 5.4 and 5.6 years old will be

`P(\text{ between 5.4 and 5.6 years old)=}(5.6-5.4)/(5.76-5)=(0.2)/(0.76)=0.2632`

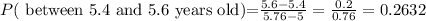
Hence, the probability that the child age is between 5.4 and 5.6 years old is 0.2632

e) If the child is at the 53rd percentile, the age of the child will be

`\begin{gathered} At\text{ 53rd percentile the age}\Rightarrow5+(53)/(100)(5.76-5) \\ =5+0.53(0.76) \\ =5.4028 \end{gathered}`

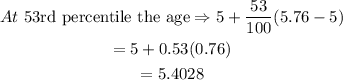
Hence, at the 53rd percentile, the age of the child is 5.4028 years old