We can solve this problem using a system of linear equations, have in mind the expression for simple interest:
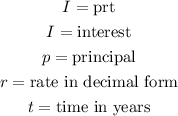
Let x be the principal invested on the first account.
Let y be the principal invested on the second account.
![\begin{gathered} x+y=30,000\rightarrow\operatorname{Re}present\text{ total invested (1)} \\ 0.08x+0.1y=2,680\rightarrow\operatorname{Re}present\text{ the rates and interest earned }(2) \end{gathered}]()
We can solve the system by the method of substitution, isolate the variable y in equation (1):
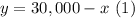
Now, substitute (1) into equation (2) to get x-value:
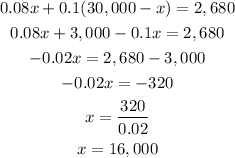
Austin invested $16,000 on the first account.
Then, substitute the x-value in the equation (1) to get y-value:
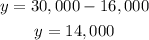
Austin invested $14,000 on the second account.