Given the quadratic equation:

The x-intercepts are the values of (x) which make the equation equal to zero
Or, the x-intercepts are the values of intersection with the x-axis
So, we will equate the equation to zero then solve it for (x):
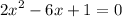
As we will not be able to factor the equation, we will use the general formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
From the equation:
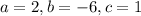
substitute with the values of {a, b, c} into the general formula:
![\begin{gathered} x=\frac{6\pm\sqrt[]{(-6)^2-4\cdot2\cdot1}}{2\cdot2}=\frac{6\pm\sqrt[]{28}}{4} \\ \\ x=\frac{6+\sqrt[]{28}}{4}=\frac{6+2\sqrt[]{7}}{4}=(3)/(2)+(1)/(2)\sqrt[]{7} \\ or \\ x=\frac{6-\sqrt[]{28}}{4}=\frac{6-2\sqrt[]{7}}{4}=(3)/(2)-(1)/(2)\sqrt[]{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l5pj64dqb1s1k4dk2u9xiouvwr37uo7tfq.png)
So, the x-intercepts are:
![x=\mleft\lbrace(3)/(2)-(1)/(2)\sqrt[]{7},(3)/(2)+(1)/(2)\sqrt[]{7}\mright\rbrace](https://img.qammunity.org/2023/formulas/mathematics/college/soqr0xy5ginx97mr0b9hhqo1t9gzjqrhvm.png)