Answer:
The greatest height is 256 Feets
Explanations:
The distance of the coin above the water is modeled by the equation:

The distance (y) is maximum when dy/dx = 0
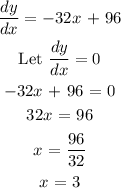
x = 3 seconds
To calculate the maximul height, substitute x = 3 into the given height equation
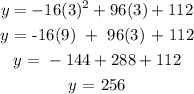
The greatest height is 256 Feet