Question

The angle 01 is located in Quadrant III, and sin(01)=-12/13. What is the value of cos(O1)

Answer 1

The cosine of the angle is -5/13 given that
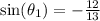`\sin(\theta_1) = -(12)/(13)`and in quadrant III

How to determine the cosine of the angle

From the question, we have the following parameters that can be used in our computation:

`\sin(\theta_1) = -(12)/(13)`

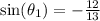
The cosine of the angle can be calculated using the following equation

`\cos(\theta_1) = \pm \sqrt{1 - \sin^2(\theta_1)`

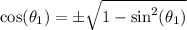
Substitute the known values into the equation

`\cos(\theta_1) = \pm \sqrt{1 - (-(12)/(13))^2`

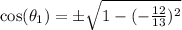
So, we have

`\cos(\theta_1) = \pm \sqrt{1 - (144)/(169)`

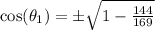
This gives

`\cos(\theta_1) = \pm \sqrt{ (25)/(169)`

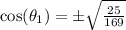
So, we have

`\cos(\theta_1) = \pm(5)/(13)`

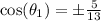
Cosine is negative in the third quadrant

So, we have

`\cos(\theta_1) = -(5)/(13)`

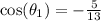
Hence, the cosine of the angle is -5/13

Answer 2

`cos\emptyset_1=\frac{5}{\text{1}3}`

Step-by-step explanation

Step 1

The angle 01 is located in Quadrant III,so

we know, by definition

`\text{sen}\varphi=\frac{opposite\text{ side}}{\text{hypotenuse}}`

so, by replacing

`\begin{gathered} \text{sen}\varphi=\frac{opposite\text{ side}}{\text{hypotenuse}} \\ \text{sen}\emptyset_1=\frac{-12}{\text{1}3} \\ \text{hence:} \\ \text{opposite side}(\text{purple) is 12( negative indicates to the left)} \\ \text{hypotenuse}=13 \end{gathered}`

to find cos , we need to find the misssing side( adjacent side), let's use the Pythagorean theorem:

`\begin{gathered} a^2+b^2=c^2 \\ so \\ 12^2+adjacentside^2=13^2 \\ adjacentside^2=13^2-12^2 \\ adjacentside^2=25 \\ √(adjacentside^2)=√(25) \\ \text{adjacent side= 5} \\ \\ \end{gathered}`

Step 2

now, replace in the cosine formula

`\begin{gathered} cos\emptyset=\frac{adjancent\text{ side}}{\text{hypotenuse}} \\ cos\emptyset_1=\frac{5}{\text{1}3} \\ \end{gathered}`

I hope this helps you