Question

Give the equation for two lines to be 4x-y=-8 and y=1/4x+10(c)Based on your answers above are the two lines parallel perpendicular or neitherWhat statement below explains your reasoning for your answer above A. The slopes are undefined B. both equations represent the same lineC. both lines have slopes the that are opposite reciprocal of each other D. the slopes are neither equal nor opposite reciprocals E. both lines have the same slope in a different Y-intercept

Answer 1

(a)Slope: 4, y-intercept: (0, 8).

(b)Slope: 1/4, y-intercept: (0, 10).

(c)Neither

(d)D. The slopes are neither equal nor opposite reciprocals.

Explanation:

Given the equations for two lines.

`\begin{gathered} 4x-y=-8 \\ y=(1)/(4)x+10 \end{gathered}`

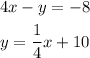
We want to find the slopes and the y-intercept in coordinate form.

In order to do this, we compare the given lines with the slope-intercept form:

`y=mx+b\text{ where m=slope, b=y-intercept}`

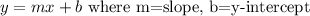
Part A

`\begin{gathered} 4x-y=-8 \\ \implies y=4x+8 \\ m=4 \\ b=8 \end{gathered}`

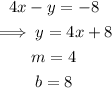
• The slope of the line, m = 4

,

• The y-intercept, (x, y) = (0, 8).

Part B

`\begin{gathered} y=(1)/(4)x+10 \\ m=(1)/(4) \\ b=10 \end{gathered}`

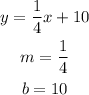
• The slope of the line, m = 1/4

,

• The y-intercept, (x, y) = (0, 10).

Part C

• Two lines are said to be ,parallel, if they have the ,same slope,.

,

• Two lines are said to be ,perpendicular, if the ,product of their slopes is -1,.

From parts (a) and (b) above:

• The slope of the first line = 4

,

• The slope of the second line = 1/4

`\begin{gathered} 4\\eq(1)/(4) \\ 4*(1)/(4)=1\\eq-1 \end{gathered}`

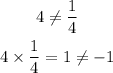
Therefore, the lines are neither.

The reason for this is that the slopes are neither equal nor opposite reciprocals. (Option D).