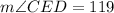Question

Help on this practice question and I will be sure

Answer 1

By definition, the measure of the angle formed by the intersection of two Chords inside a circle, is equal to the sum of the intercepted Arcs divided by 2.

In this case you can identify that this is an angle formed when the two chords of the circle intersect:

`\angle CED`

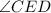
These angles are also formed by that intersection:

`\begin{gathered} \angle BED \\ \angle AEC \\ \angle AEB \end{gathered}`

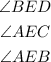
Knowing the explained above, you can set up the following equation:

`m\angle BED=m\angle AEC=(87\degree+35\degree)/(2)`

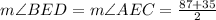
Evaluating, you get:

`\begin{gathered} m\angle BED=m\angle AEC=(122\degree)/(2) \\ \\ m\angle BED=m\angle AEC=61\degree \end{gathered}`

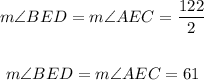
Notice that:

-The angles BED and AEC are Vertical angles.

- The angles CED and AEB are Vertical angles.

By definition, Vertical angles share the same vertex and they are congruent.

Knowing the explained above and also knowing that there are 360 degrees in a circle, you can set up the following equation:

`61\degree+61\degree+m\angle CED+m\angle AEB=360\degree`

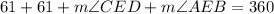
Since:

`m\angle CED=m\angle AEB`

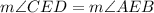
You can rewrite the equation as following:

`61\degree+61\degree+m\angle CED+m\angle CED=360\degree`

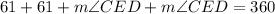
Solving for the angle CED, you get:

`\begin{gathered} 122\degree+m\angle CED+m\angle CED=360\degree \\ m\angle CED+m\angle CED=360\degree-122\degree \\ \\ m\angle CED=(238\degree)/(2) \\ \\ m\angle CED=119\degree \end{gathered}`

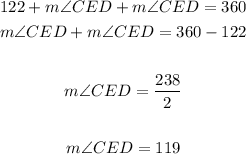
The answer is:

`m\angle CED=119\degree`