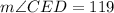By definition, the measure of the angle formed by the intersection of two Chords inside a circle, is equal to the sum of the intercepted Arcs divided by 2.
In this case you can identify that this is an angle formed when the two chords of the circle intersect:
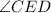
These angles are also formed by that intersection:
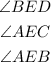
Knowing the explained above, you can set up the following equation:
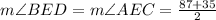
Evaluating, you get:
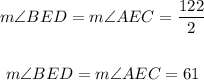
Notice that:
-The angles BED and AEC are Vertical angles.
- The angles CED and AEB are Vertical angles.
By definition, Vertical angles share the same vertex and they are congruent.
Knowing the explained above and also knowing that there are 360 degrees in a circle, you can set up the following equation:
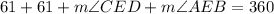
Since:
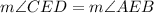
You can rewrite the equation as following:
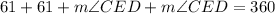
Solving for the angle CED, you get:
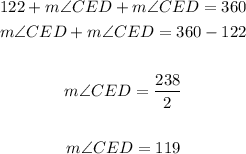
The answer is: