The volume of a cube is the product of its dimensions. Since all three dimensions have the same length, we just need to multiply the length of one dimension 3 times.
So if one dimension of the building block is equal 1/12x^2, we have that:
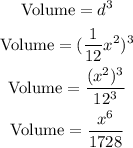
So the volume of the building block is equal (1/1728)x^6.