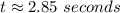Given that the ball's height (in feet) after seconds is given by the following equation:
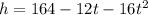
You can determine that when the ball hits the ground:
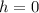
Then, you can substitute that value into the equation:
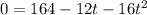
In order to find the values of "t", you can follow these steps:
1. Rewrite it in the form:

Then:
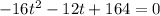
2. Use the Quadratic Formula:
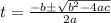
In this case:

Therefore, you can substitute values into the formula and evaluate:
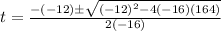
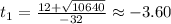
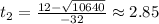
Choose the positive value:
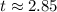
Hence, the answer is: