Question

Suppose you deposit $2,000 in a savings account that pays interest at an annual rate of 4%. If no money is added or withdrawn from the account, answer the following questions. a. How much will be in the account after 4 years? b. How much will be in the account after 18 years? c. How many years will it take for the account to contain $2,500? d. How many years will it take for the account to contain $3,000? a. After 4 years, the amount in the account will be $

Answer 1

Suppose you deposit $2,000 in a savings account that pays interest at an annual rate of 4%. If no money is added or withdrawn from the account, answer the following questions. a. How much will be in the account after 4 years? b. How much will be in the account after 18 years? c. How many years will it take for the account to contain $2,500? d. How many years will it take for the account to contain $3,000?

we know that

The simple interest formula is equal to

`A=P(1+rt)`

`A=P\mleft(1+rt\mright)`

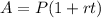
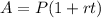
where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest

t is Number of Time Periods

in this problem we have

Part a) How much will be in the account after 4 years?

we have

P=$2,000

r=4%=0.04

t=4 years

substitute the given values

`\begin{gathered} A=2,000(1+0.04\cdot4) \\ A=\$2,320 \end{gathered}`

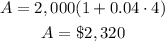
Part b How much will be in the account after 18 years?

we have

P=$2,000

r=4%=0.04

t=18 years

substitute the given values

`\begin{gathered} A=2,000(1+0.04\cdot18) \\ A=\$3,440 \end{gathered}`

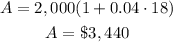
Part c How many years will it take for the account to contain $2,500?

we have

P=$2,000

r=4%=0.04

t=? years

A=$2,500

substitute

`\begin{gathered} 2,500=2,000(1+0.04\cdot t) \\ (2,500)/(2,000)=1+0.04t \\ \\ 0.04t=(2,500)/(2,000)-1 \\ t=6.25\text{ years} \end{gathered}`

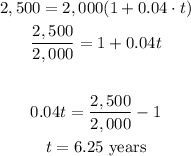
Part d How many years will it take for the account to contain $3,000?

we have

P=$2,000

r=4%=0.04

t=? years

A=$3,000

substitute

`\begin{gathered} 3,000=2,000(1+0.04\cdot t) \\ (3,000)/(2,000)=1+0.04t \\ \\ 0.04t=(3,000)/(2,000)-1 \\ t=12.5\text{ years} \end{gathered}`