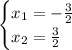Question

Quadratic equations Solve each equation. 3x^2+2=11-x^2

Answer 1

We want to find the solutions for the following quadratic equation

`3x^2+2=11-x^2`

We can start by adding x² to both sides of the equation.

`\begin{gathered} 3x^2+2+x^2=11-x^2+x^2 \\ 4x^2+2=11 \end{gathered}`

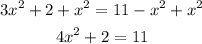
Now, we can subtract 11 from both sides.

`\begin{gathered} 4x^2+2-11=11-11 \\ 4x^2-9=0 \end{gathered}`

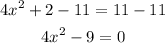
We could solve it by using the Bhaskara formula, but I'm going to use the difference of squares property.

When you have a subtraction between two squares, you can factorize them as a product of binomials

`a^2-b^2=(a+b)(a-b)`

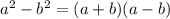
Using this property in our equation, we have

`\begin{gathered} 4x^2-9=0 \\ (2x)^2-3^2=0 \\ (2x+3)(2x-3)=0 \end{gathered}`

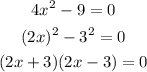
Since we have a product that results in zero, this means that at least one of the factors must be zero, therefore, the solutions of this equation are also the solutions for the following equations

`\begin{cases}2x+3=0 \\ 2x-3=0\end{cases}`

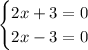
The possible values for x are

`\begin{cases}x_1=-(3)/(2) \\ x_2=(3)/(2)\end{cases}`