Question

Determine the remaining sides and angles of the triangle ABCwhat is the measure of angle Bwhat is the length of side awhat is the length of side b

Answer 1

Angles A, B, and C together add to 180 degrees.

We can find Angle B:

`\begin{gathered} 100.4+38.1+\angle B=180 \\ 138.5+\angle B=180 \\ \angle B=41.5\degree \end{gathered}`

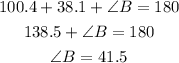
side a is opposite angle A, side b is opposite angle B.

We now have pairs for which we can solve for a side [either a or b].

We will use sin rule, which is:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

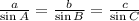
Let's find a first using known and unknown pairs:

`\begin{gathered} (a)/(\sin A)=(c)/(\sin C) \\ (a)/(\sin38.1)=(48.4)/(\sin 100.4) \\ a\sin 100.4=48.4\sin 38.1 \\ a=(48.4*\sin 38.1)/(\sin 100.4) \\ a=30.36 \end{gathered}`

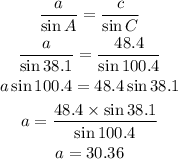
By similar process, we find b:

`\begin{gathered} (b)/(\sin B)=(c)/(\sin C) \\ (b)/(\sin41.5)=(48.4)/(\sin 100.4) \\ b\sin 100.4=48.4\sin 41.5 \\ b=(48.4*\sin 41.5)/(\sin 100.4) \\ b=32.61 \end{gathered}`

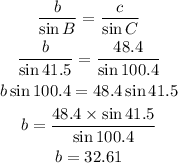
Angle B = 41.5 degrees

Side a = 30.36

Side b = 32.61