The final speed of the ball can be given as,
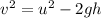
At the maximum height the final speed is zero.
Plug in the known values,
![\begin{gathered} (0m/s)^2=u^2-2(9.8m/s^2)(57.0\text{ m)} \\ u^2=2(9.8m/s^2)(57.0\text{ m)} \\ u=\sqrt[]{1117.2m^2s^(-2)} \\ =33.4\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/3zkfbl9t3o3mn2xmaf4wiyjtccp2lpz5bx.png)
Therefore, the speed with which the ball was kicked is 33.4 m/s.
Also, the final speed of the ball can be expressed as,
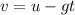
Plug in the known values,
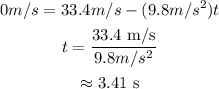
The total time flight time of the ball is calculated as,
![undefined]()
Therefore, the total flight time of the ball is 3.41 s.