Question

please help also, while doing the question please don't put a decimal answer ( ex: 1.5) because my teacher told me that's incorrect, you can add or subtract depending on the question, or check if you need to simplify!

Answer 1

Notice that the line divides each unit segment in 4 parts. Assuming that each part has the same length, then we know that each mark is equal to:

`(1)/(4)`

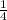
Count the amount of bottles on each mark and add the corresponding volumes to find the total volume of soda.

There are 2 bottles of soda at 1/4.

There is 1 bottle of soda at 3/4.

There is 1 bottle of soda at 4/4

There is 1 bottle of soda at 5/4

There are 2 bottles of soda at 6/4.

Add all the fractions to find the total volume:

`(1)/(4)+(1)/(4)+(3)/(4)+(4)/(4)+(5)/(4)+(6)/(4)+(6)/(4)=(1+1+3+4+5+6+6)/(4)=(26)/(4)`

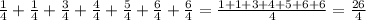
Simplify the fraction 26/4, since both numerator and denominator are multiples of 2:

`(26)/(4)=(26/2)/(4/2)=(13)/(2)`

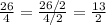
The fraction 13/2 represents the total volume of soda. Since that volume is re-distributed equally into the 7 bottles, divide 13/2 by 7 to find the volume that each bottle will have:

`(13)/(2)/7=(13)/(2)/(7)/(1)=(13)/(2)*(1)/(7)=(13)/(2*7)=(13)/(14)`

Therefore, 13/14 new flavor of soda was poured into each bottle.