We have an unknown quantity, which is y. We are told that it varies joint as a and b. This translates as follows
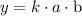
where k is a constant.
Now, we are also told that it varies inversely as the square root of c. So this look as follows
![y=\frac{k}{\sqrt[]{c}}](https://img.qammunity.org/2023/formulas/mathematics/college/s4pjgugxr3cddciqksm0gw176gb8n12qlz.png)
where k is another constant. We have to combine both facts as follows
![y=\frac{k\cdot a\cdot b}{\sqrt[]{c}}](https://img.qammunity.org/2023/formulas/mathematics/college/3q8chjghverrt7r42jqxkso3y4jx1hmbd6.png)
in this case, k is a constant. Now, we are told that whenever c=4, b=2 and a=6 we get y=24. So we get the following equation
![24=\frac{k\cdot6\cdot2}{\sqrt[]{4}}=(k\cdot6\cdot2)/(2)=6\cdot k](https://img.qammunity.org/2023/formulas/mathematics/college/9l24u1xitns9wvvlsppoc9jts2az3584c8.png)
By dividing by 6 on both sides, we get
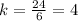
So the general expression of y looks like this
![y=\frac{4\cdot a\cdot b}{\sqrt[]{c}}](https://img.qammunity.org/2023/formulas/mathematics/college/9fqdzbc3e01zw5e0qnhh14xwzyvizxa250.png)
Now, we want to calculate the value of y whenever a=3 and b=5 and c=25. So we get
![y=\frac{4\cdot3\cdot5}{\sqrt[]{25}}=(4\cdot3\cdot5)/(5)=4\cdot3=12](https://img.qammunity.org/2023/formulas/mathematics/college/zk2nof0b0oi91tgjxgv3c8mmmfhhrpd6wp.png)
so y=12 whenever a=3, b=5 and c=25.