Given
radius of the circle is 10 units.
Center(3,-1)
Find
equation of the circle.
Step-by-step explanation
As we know that the equation of the circle is given by

where (h , k) is the center and r is a radius.
so , equation of the circle =
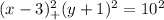
Final Answer
The equation of the circle =
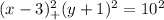
so , the correct option is 4.