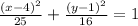Given:
Center ==> (4, 1)
Length = 8
c = 3
Let's find the equation for the given ellipse that statisfies the conditions above.
Take the equation:
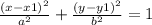
Here, we have a vertical minor axis with points: (x, y) ==> (4, 1) which has the equation below:
Substitute 4 for x1 and substitute 1 for y1
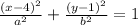
Where:

Since the minor axis is vertical and has a length of 8, we have:

Given: c = 3
To find the value of a, substitute 3 for c and 4 for b:
![\begin{gathered} c^2=a^2+b^2^{} \\ \\ 3^2=a^2-4^2 \\ \\ \text{Add 4}^2\text{ to both sides:} \\ 3^2+4^2=a^2-4^2+4^2 \\ \\ 3^2+4^2=a^2 \\ \\ \text{Take the square root of both sides:} \\ \sqrt[]{3^2+4^2}=\sqrt[]{a^2} \\ \\ \sqrt[]{3^2+4^2}=a \\ \\ \sqrt[]{9+16}=a \\ \\ \sqrt[]{25}=a \\ \\ 5=a \\ \\ a=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hg3vlfvwxjoldskk4nasp4wq45atqwy5n1.png)
Therefore, from the general equation, substitute 5 for a, and 4 for b
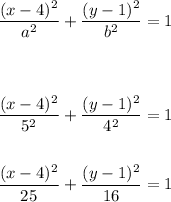
Therefore, the equation for thr given ellipse that satisfies the given conditions is:
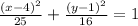
ANSWER: