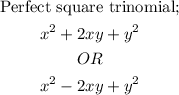W e shall match the following definitions to the appropriate headings;
(1)
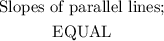
The slopes of parallel lines are always equal in value
(2)
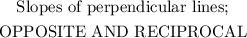
The slope of a line perpendicular to another line is a negative and at the same time a reciprocal (that is, negative inverse) of the other line.
A line with slope 3, would have a perpendicular with slope of
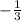
(3)
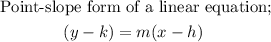
In this case the point
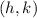
are the coordinates for the given point, while m is the slope also given.
(4)
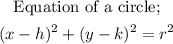
(5)
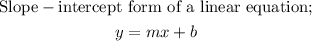
Where m is the slope and b is the y-intercept.
(6)
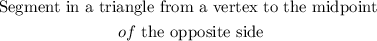
(7)

(8)
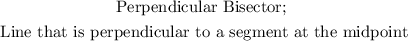
(9)