PART 1
To traslate a point 4 units to the left, we substract 4 from the x-coordinate. Similarly, to traslate it 8 units up we add 8 to the y-coordinate.
This way, the rule for translating a point 4 units left and 8 units up is:
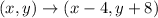
PART 2
Let's apply the traslation to each of the vertex:
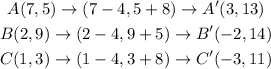
This way, we can conclude that the new set of vertex is:
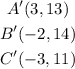
PART 3
By definiton, the rule to reflect a point over the y-axis is:
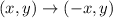
PART 4
We apply this transformation to each of the new vertex:
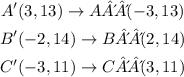
This way, we can conclude that the new set of vertex is:
PART 5
We can conclude that A HAS NOT returned to its original location.