Question

ΔABC is translated 4 units to the left and 8 units up, then reflected across the y-axis. Answer the questions to find the coordinates of A after the transformations.1. Give the rule for translating a point 4 units left and 8 units up.2. After the translation, where is A located?3. Give the rule for reflecting a point over the y-axis.4. What are the coordinates of A after the reflection?5. After the two transformations, has A returned to its original location?

Answer 1

PART 1

To traslate a point 4 units to the left, we substract 4 from the x-coordinate. Similarly, to traslate it 8 units up we add 8 to the y-coordinate.

This way, the rule for translating a point 4 units left and 8 units up is:

`(x,y)\rightarrow(x-4,y+8)`

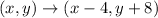
PART 2

Let's apply the traslation to each of the vertex:

`\begin{gathered} A(7,5)\rightarrow(7-4,5+8)\rightarrow A^(\prime)(3,13) \\ B(2,9)\rightarrow(2-4,9+5)\rightarrow B^(\prime)(-2,14) \\ C(1,3)\rightarrow(1-4,3+8)\rightarrow C^(\prime)(-3,11) \end{gathered}`

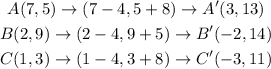
This way, we can conclude that the new set of vertex is:

`\begin{gathered} A^(\prime)(3,13) \\ B^(\prime)(-2,14) \\ C^(\prime)(-3,11) \end{gathered}`

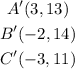
PART 3

By definiton, the rule to reflect a point over the y-axis is:

`(x,y)\rightarrow(-x,y)`

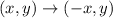
PART 4

We apply this transformation to each of the new vertex:

`\begin{gathered} A^(\prime)(3,13)\rightarrow A´´(-3,13) \\ B^(\prime)(-2,14)\rightarrow B´´(2,14) \\ C^(\prime)(-3,11)\rightarrow C´´(3,11) \end{gathered}`

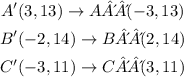
This way, we can conclude that the new set of vertex is:

`\begin{gathered} A´´(-3,13) \\ B´´(2,14) \\ C´´(3,11) \end{gathered}`

PART 5

We can conclude that A HAS NOT returned to its original location.