To find the rate of change we need to find the derivative of the function. The derivative of an exponential function is:
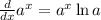
Then in our case we have:
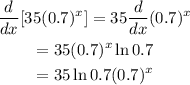
Now we evaluate the derivative at the point x=0, then:
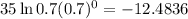
Therefore the rate of change is appoximately -12.4836.