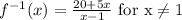Given the function:
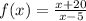
Let's solve for the following:
• (a). The inverse of the function.
Rewrite f(x) for y
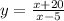
Interchange the variables:
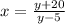
Solve for y:
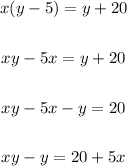
Factor the left side:
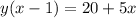
Divide both sides by (x - 1):
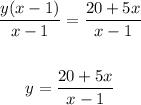
Therefore, the inverse of the function:
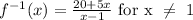
Part B.
Now, let's verify the following:
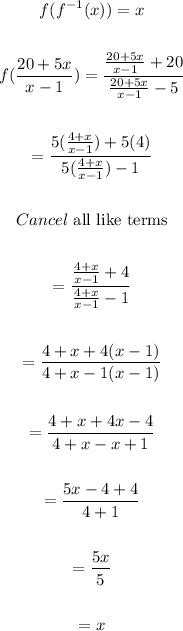
Therefore, we have:
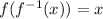
Also, let's verify f¯¹(f(x)) = x:
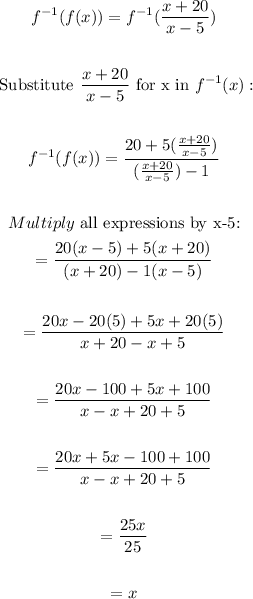
Therefore, we have:
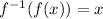
ANSWER:
Part A: C