Question

2. Great America has recently designed a roller coaster as seen below. The mass of the cart is 100 kg and the track has one hill followed by a circular loop with a 15 meter radius. (a)What minimum speed must the cart move to make it through the top of the loop? (b) The cart starts at rest on top of the hill before speeding through the loop. How tall must they make the hill so that the roller coaster has enough PE to make it through the loop.

Answer 1

Given:

The mass of the cart is m = 100 kg

The radius of the track is r = 15 m

To find

(a) Minimum speed required to reach the top of the loop

(b) The height of the hill

Step-by-step explanation:

(a) The formula to calculate minimum speed is

`v_(min)=√(gr)`

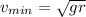
Here, g = 9.8 m/s^2 is the acceleration due to gravity.

On substituting the values, the minimum speed will be

`\begin{gathered} v_(min)=√(9.8*15) \\ =12.13\text{ m/s} \end{gathered}`

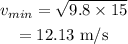
(b) The height of the hill required to make it through the loop is

`\begin{gathered} mgh=(1)/(2)m(v_(min))^2 \\ h=((v_(min))^2)/(2g) \\ =\text{ 7.5 m} \end{gathered}`