In order to find the angle between the lines, first solve each given equation for y, as follow:
2x + 3y = 5 subtract 2x both sides
3y = -2x + 5 divide by 3 both sides
y = -2/3 x + 5/3
x - 3y = 6 subtract x both sides
- 3y = -x + 6 divide by -3 both sides
y = 1/3 x - 2
next, take into account that the general equation of a line can be written as follow:
y = mx + b
where m is the slope and b the y-intercept.
Consider that the tangent of the inclination angle of the line is equal to the slope of the line.
You can notice that the slopes of the lines are m1 = -2/3 and m2 = 1/3 respectively.
Then, you have:
tanθ1 = -2/3
tanθ2 = 1/3
apply inverse tangent to the previous equations to get the values of the angles:
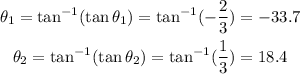
the difference in the angles is the angle between both lines:
18.4 - (33.7) = 18.4 + 33.7 = 52.1
Hence, the angle between the lines is 52.1 degrees