Question

A certain disease has an incidence rate of 0.9%. If the false-negative rate is 4% and the false positive rate is 2%, compute the probability that a person who tests positive actually has the disease___. Give your answer accurate to at least 3 decimal places ___.

Answer 1

Let's suppose you have a population of 1000 people.

If the incidence rate of the disease is 0.9%, it means that 1000(0.009) = 9 people will have the disease

It means that 991 people will not have the disease.

Of the 9 people who have the disease, 4% of them will test negative, then 9(0.04) = 0.36 people will test negative, so the remaining 8.64 people will test positive.

Of the 991 people who don't have the disease, 991(0.02) = 19.82 people will test postive.

Then, the probability will be:

`\begin{gathered} \frac{8.64\text{ truly positives}}{28.46\text{ total positives}} \\ =\text{ 0.30358} \\ =0.30358\text{ \lparen100\%\rparen} \\ =30.358\text{ \%} \end{gathered}`

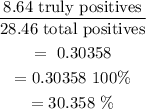
The probability is 0.30358 or 30.358%