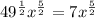Step-by-step explanation:
Question 2
To answer the question, we will use the exponential laws
![\begin{gathered} a^{(1)/(b)}=\sqrt[b]{a} \\ a^(-1)=(1)/(a) \\ a^{(b)/(c)}=\sqrt[c]{a^b} \\ a^b* a^c=a^(b+c) \\ a^b/ a^c=a^(b-c) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/38fa7svgvynhml34wdinak6momt90dftz0.png)
Applying these laws
Question 2a
![\sqrt[4]{(mn)^(12)}=(mn)^{(12)/(4)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/xf11corpr076uw2x1j9o7rwc6m9jicm623.png)
![\sqrt[4]{(mn)^(12)}=(mn)^{(12)/(4)}=(mn)^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/n1wuq2wwfavj9zytq5rrsio0476g4ej8hc.png)
Question 2b
![√(x).\sqrt[7]{x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/flabbrjklp961mmzjq8h9d9761aadjb2u2.png)
we will rewrite it as
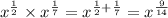
Question 2c
![\frac{\sqrt[6]{x}}{\sqrt[4]{x}}=\frac{x^{(1)/(6)}}{x^{(1)/(4)}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/eiwed3jpplhzp6jh9t48dv0go1xw2halv6.png)
Then
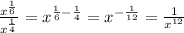
Question 2d
![\sqrt[6]{(r^6)/(s^(18))}=((r^6)/(s^(18)))^{(1)/(6)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ugac20vpowbctncahayrh6kw1vnbxrqsxq.png)
Simplifying further
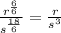
Question 2e
![\sqrt[3]{x^6q^9}=(x^6q^9)^{(1)/(3)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9oydo5691trbxq1kjskmj6vypy4n7da8vm.png)
Simplifying further
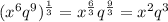
Question 2f
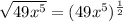
Simplifying further