The given expression is-
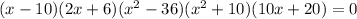
This expression shows five factors. Using the zero-product property we can find all five solutions.
![\begin{gathered} x-10=0\rightarrow x=10 \\ 2x+6=0\rightarrow2x=-6\rightarrow x=-3 \\ x^2-36=0\rightarrow x^2=36\rightarrow x=\pm6 \\ x^2+10=0\rightarrow x^2=-10\rightarrow x=\sqrt[]{-10} \\ 10x+20=0\rightarrow10x=-20\rightarrow x=-(20)/(10)=-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qm2vqjysy9axrg1qoesqw722qs2h495jd1.png)
Therefore, there are 4 real solutions and one imaginary solution, respectively, they are 10, -3, 6 and -6, -2, and the square root of negative 10.