Question

A small shop buys sweets at 2.15 € each.Her expenses are € 53,500 and she sells each unit for € 3.How many units must she sell to make a profit of € 51,000.

Answer 1

The first thing we have to do is identify our variables to determine the equation that describes the problem.

• $2.15, price of the sweets for buy

,

• $3.00, price of the sweets for sell

,

• $53,500, initial expense

,

• $51,000, final gain

,

• x, number of sweets

,

• Tm, Total of money

,

• Sg, Sweet gain

We have a single variable then and we know that we have to know what is the total amount of money that we must generate to obtain this profit, for this we add our initial expense with the final desired profit

`\begin{gathered} 53,500+51,000=Tm \\ Tm=104,500 \end{gathered}`

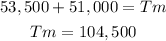
know when we will earn for each candy we must subtract the purchase price from the sale price:

`\begin{gathered} Sg=3.00-2.15 \\ Sg=0.85 \end{gathered}`

Now if our final equation will be to find the number of candies that multiplied by the profit of the caramel charge the total value of money that we need

The answer is: You have to sell 122,941 sweets to generate a profit of $51,000