Question

The width of a rectangle is 4 less than the length. If the area of the rectangle is 165cm?,solve for the length and width of the rectangle.

Answer 1

length:15 cm

width: 14 cm

Step-by-step explanation

Step 1

Let

w represents the width of the rectangle

l represents the length of the rectangle

a)The width of a rectangle is 4 less than the length,hence

write this in math terms, replace

`\begin{gathered} \text{width}=length-4 \\ w=l-4\rightarrow equation\text{ (1)} \end{gathered}`

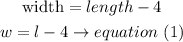
b)the area of the rectangle is 165 square cm

the area of a rectangle is given by

`\begin{gathered} \text{Area}=\text{length}\cdot\text{width} \\ \text{replace} \\ 165cm^2=l\cdot w\rightarrow \\ 165=l\cdot w\rightarrow equiation(2) \end{gathered}`

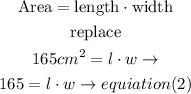
Step 2

now, solve the equations

`\begin{gathered} w=l-4 \\ 165=lw \end{gathered}`

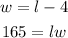
a) replace the w from equation (1) into equation(2)

`\begin{gathered} 165=lw \\ 165=l(l-4) \\ 165=l^2-4l \\ \text{subtract 165 on both sides} \\ 165-165=l^2-4l-165 \\ l^2-4l-165=0 \end{gathered}`

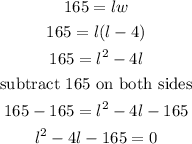
b) now, we have a quadratic equation in the form

`ax^2+bx+c=0`

hence, we can use the quadratic formula to solve

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

let

a=1

b=-4

c=-165

replace

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-4)\pm\sqrt[]{-4^2-4(1)(-165)}}{2\cdot1} \\ x=\frac{4\pm\sqrt[]{676}}{2}=x=(4\pm26)/(2) \end{gathered}`

therefore

`\begin{gathered} x=(4\pm26)/(2) \\ x_1=(4+26)/(2)=(30)/(2)=15 \\ x_2=(4-26)/(2)=(-22)/(2)=-11 \end{gathered}`

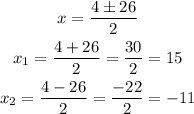
as we are searchinf for a distance, the only valid answer is 15

so, the answer is length= 15 cm

`l=15\text{ cm}`

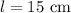
c) finally, replace the l value into equation (1) to find the width

`\begin{gathered} w=l-4\rightarrow equation\text{ (1)} \\ w=15-4 \\ w=11 \end{gathered}`

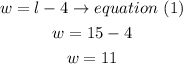
therefore, the width is 11 centimeters

I hope this helps you