length:15 cm
width: 14 cm
Step-by-step explanation
Step 1
Let
w represents the width of the rectangle
l represents the length of the rectangle
a)The width of a rectangle is 4 less than the length,hence
write this in math terms, replace
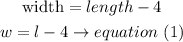
b)the area of the rectangle is 165 square cm
the area of a rectangle is given by
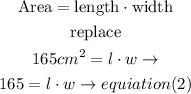
Step 2
now, solve the equations
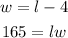
a) replace the w from equation (1) into equation(2)
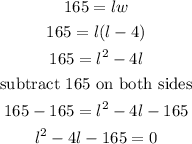
b) now, we have a quadratic equation in the form
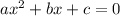
hence, we can use the quadratic formula to solve
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
let
a=1
b=-4
c=-165
replace
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-4)\pm\sqrt[]{-4^2-4(1)(-165)}}{2\cdot1} \\ x=\frac{4\pm\sqrt[]{676}}{2}=x=(4\pm26)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/41qtpr3opokpkx221cunkvfsjub73jzv77.png)
therefore
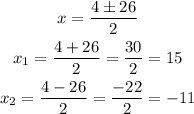
as we are searchinf for a distance, the only valid answer is 15
so, the answer is length= 15 cm
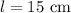
c) finally, replace the l value into equation (1) to find the width
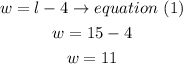
therefore, the width is 11 centimeters
I hope this helps you