Question

Write an equation for each line.(1). y-intercept -2.1, x-intercept of 3.5(2). through (1.2, 5.1), x-intercept of 3.7

Answer 1

hello

since we're given y and x intercept, we can use it to find the slope of the equation

y-intercept = 2.1

x-intercept = 3.5

what this implies that in a given graph, y-axis is (0, 2.1) and x-axis (3.5, 0)

now we can use this co-ordinate to find our slope

so our odered pair are (3.5, 0) and (0, 2.1)

`\text{slope}=\frac{y_2-y_1}{x_2-x_1_{}}`

y2 = 2.1

y1 = 0

x2 = 0

x 1 = 3.5

`\begin{gathered} \text{slope}=(2.1-0)/(3.5-0) \\ \text{slope}=(2.1)/(3.5) \\ \text{slope}=0.6=(3)/(5) \end{gathered}`

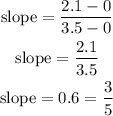
now we know our slope as 3/5

we can use this slope to find the equation of the line

remember our y-intercept = 2.1

equation of staright line is given as y = mx + c

m = slope

c = y-intercept

now, the equation of this line is

y = 3/5x + 2.1

`y=(3)/(5)x+2.1`

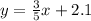
b.

we have one point (1.2, 5.1) and an x-intercept of 3.7

let the first point (1.2, 5.1) be A and the second point as B

A = (1.2, 5.1)

B = (3.7, 0)

y2 = 0

x2 = 3.7

y1 = 5.1

x1 = 1.2

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_(\square)) \\ \text{slope}=(0-5.1)/(3.7-1.2) \\ \text{slope}=-(5.1)/(2.5) \\ \text{slope}=-2.04 \end{gathered}`

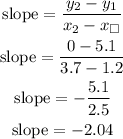
y = mx + c

m = slope

c = y-intercept

let's use co-ordinate B to find our y-intercept

`\begin{gathered} y=mx+c \\ 0=-2.04(3.7)+c \\ \text{solve for c} \\ 0=-7.548+c \\ c=7.548 \end{gathered}`

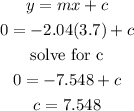
we can now re-write our equation with the standard form of y = mx + c

y = -2.04x + 7.548